How To Predict The Resistance Of A Thermistor At Different Temperatures

The resistance of a small bead thermistor varies inversely with its temperature. In other words - as the temperature rises the resistance falls. And as the temperature falls the resistance rises. Consequently - the actual resistance of the thermistor will only coincide with its marked value - at one particular temperature - usually 25°C (77°F).

To calculate the resistance of the thermistor at other temperatures - you need two pieces of information. One is an accurate resistance measurement - taken at a known temperature. And the second is the value of a constant - called Beta. It defines the relationship between changes in temperature and changes in resistance.

Unfortunately - you can't rely on the colour code to provide you with the resistance measurement. Manufacturing tolerances mean that the nominal value of the thermistor can be out by as much as ą 20%.

And - although Beta is described as a constant - its value actually varies from one batch of thermistors to the next. You will find published values for Beta. But these are only typical values - not actual values. And they are only valid for a limited part of the temperature scale. Usually from 25°C (77°F) to 85°C (185°F).

Since the marked value of the thermistor and the figure for Beta are both unreliable - the outcome of any calculations will also be unreliable. In other words - using the published data to predict the value of your thermistor - is a waste of time.

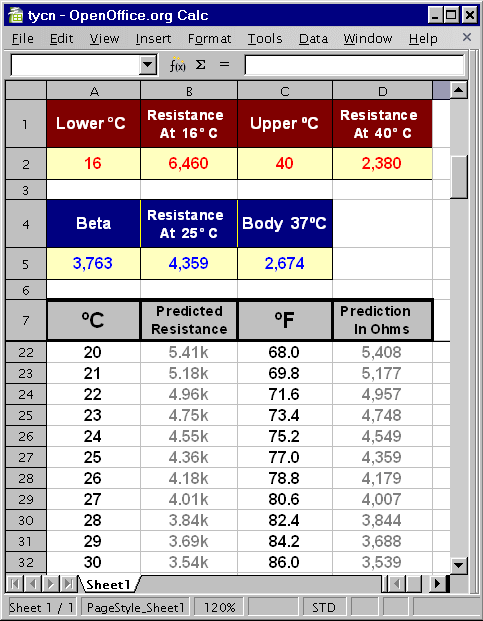
What you really need is reliable data - that's derived directly from your own particular thermistor. That is - two accurate resistance measurements - taken at two different temperatures. The spreadsheet will then use this data to calculate the real value of Beta - and to predict the resistance of your thermistor over a range of temperatures.

The predictions will be at their most accurate - around and between the two temperatures you've chosen. I achieved an accuracy of better than ą 1%. However - the results will only be as good as the quality of your input data. At the bottom of the page - there are a few tips on how to make that data as accurate as possible.

How To Use The Spreadsheet
	The Zip file contains both OpenOffice and MS Works spreadsheets. Two versions of each type are available - one is in °C - and the other is in °F. So you can choose both the software you want to use - and the units in which you prefer to work. You don't have to understand the maths in order to use the spreadsheet. ============ You'll need two resistance values - taken at two different temperatures. I measured my two resistances at 16°C and 40°C. But you can choose your own two temperatures. ============ The predictions will be at their most accurate between and around your two chosen temperatures. So choose temperatures that bracket the area of the scale you're using in your project. Enter your temperature readings - and the corresponding resistance values - into the first four boxes of Row 2. The spreadsheet will do the rest. ============ It uses your figures to calculate the actual value of Beta - in the neighbourhood of the chosen temperatures. Then it predicts the resistance of the thermistor between - and a little beyond - those two temperatures. That is - from 10°C (20°F) below the Lower temperature - to 10°C (20°F) above the Upper temperature. ============ You can extend this range of predictions artificially - though it's likely to have some effect on accuracy. Make a note of the highest and/or the lowest temperatures in the spreadsheet - together with their predicted resistances in ohms. Then re-insert these values into the relevant boxes of Row 2 - in place of your actual measured data. This will extend the range of predictions in the spreadsheet by a further 10°C (20°F) - above and/or below. If you go on doing this - you can extend the range of predictions even further. ============ The spreadsheet includes a specific prediction for 25°C (77°F). That's the temperature at which the resistance of the thermistor - should equal its nominal colour code markings. If 25°C (77°F) is in the neighbourhood of your two input temperatures - you can use the prediction to test the accuracy of the colour code markings. ============ My thermistor was suppose to have a resistance of 4k7 at 25°C But the actual resistance at 25°C was more like 4k3. I have other thermistors that are closer to their nominal values. But I chose this one to illustrate how manufacturing tolerances can produce a significantly different value. ============ I've also included the prediction for body temperature. If it's in the neighbourhood of your two input temperatures - you can use it to test the accuracy of your input data. Put the thermistor under your arm - and wait for the meter reading to stabilize. This may take some time. You can check the accuracy of your thermometer in the same way. ============

How To Use The Spreadsheet

The Zip file contains both OpenOffice and MS Works spreadsheets.

Two versions of each type are available - one is in °C - and the other is in °F.

So you can choose both the software you want to use - and the units in which you prefer to work.

You don't have to understand the maths in order to use the spreadsheet.

              ============

You'll need two resistance values - taken at two different temperatures.

I measured my two resistances at 16°C and 40°C.

But you can choose your own two temperatures.

              ============

The predictions will be at their most accurate between and around your two chosen temperatures.

So choose temperatures that bracket the area of the scale you're using in your project.

Enter your temperature readings - and the corresponding resistance values -  into the first four boxes of Row 2.

The spreadsheet will do the rest.

              ============

It uses your figures to calculate the actual value of Beta - in the neighbourhood of the chosen temperatures.

Then it predicts the resistance of the thermistor between - and a little beyond - those two temperatures.

That is - from 10°C (20°F) below the Lower temperature - to 10°C (20°F) above the Upper temperature.

              ============

You can extend this range of predictions artificially - though it's likely to have some effect on accuracy.

Make a note of the highest and/or the lowest temperatures in the spreadsheet - together with their predicted resistances in ohms.

Then re-insert these values into the relevant boxes of Row 2 - in place of your actual measured data.

This will extend the range of predictions in the spreadsheet by a further 10°C (20°F) - above and/or below.

If you go on doing this - you can extend the range of predictions even further.

              ============

The spreadsheet includes a specific prediction for 25°C (77°F).

That's the temperature at which the resistance of the thermistor - should equal its nominal colour code markings. 

If 25°C (77°F) is in the neighbourhood of your two input temperatures - you can use the prediction to test the accuracy of the colour code markings.

              ============

My thermistor was suppose to have a resistance of 4k7 at 25°C

But the actual resistance at 25°C was more like 4k3.

I have other thermistors that are closer to their nominal values.

But I chose this one to illustrate how manufacturing tolerances can produce a significantly different value.

              ============

I've also included the prediction for body temperature. 

If it's in the neighbourhood of your two input temperatures - you can use it to test the accuracy of your input data.

Put the thermistor under your arm - and wait for the meter reading to stabilize.

This may take some time.

You can check the accuracy of your thermometer in the same way.

              ============

Predicting Thermistor Resistance

Making Accurate Readings

Formulas Used In The Spreadsheet

OpenOffice Software